A Physicist’s Best Friend: Fermi Questions
Winter
2017
Physics Puzzler
A Physicist’s Best Friend: Fermi Questions
How many piano tuners are in Chicago?
By:Brad R. Conrad, PhD, Director, Society of Physics Students & Sigma Pi Sigma
Enrico Fermi would famously ask his introductory course students to answer that question, without aid of book (or Internet). This seemingly impossible task can be accomplished in several different ways, with only background knowledge. The results, while not precise, should be excellent estimates, provide the scale of the correct values, and agree with the actual solution within at least an order of magnitude.
Of course, it isn’t important to know exactly how many piano tuners there are in a city. You can simply look it up! What is important is to be able to estimate an unknowable quantity quickly and logically. The real goal is to know, “About how many?” to get a sense of what we might expect if we could look up the answer: Is it two? Ten? Five hundred? Ten thousand?
Physics is a wonderfully messy science, full of these back-of-the-envelope questions. We often seek to see if something is even possible or, roughly, how big are we talking? Is the electric field strong enough? How much current do we need? Could we even reach that temperature? What value do I even expect? Through the use of logic, estimation, and reasonable assumptions, we can often determine a quantity to within an order of magnitude, or if we are good, maybe even a factor of 2, with just a pen and something to write on.
"Back-of-the-envelope" calculations are often a physicist’s first line of attack against the unknown. They are so important that they are commonly asked in technical interviews because the process of generating a solution is an excellent, on-your-feet test of reason and intellectual skill.
Let’s Give it a Try: Coffee Consumption
Here is an example near and dear to my heart: Many physicists are known to drink a lot of coffee. If we could brew coffee in swimming pools, how many pools would we need to satisfy the need in the U.S. on a given day?

Solution:
Nobody knows the “real” answer to this question because no one would ever brew coffee in swimming pools! Below is one solution I came up with, but keep in mind there are many other ways of arriving at an answer, and not all solutions are equally good.
First, we must answer the following question: What do I need to know to answer this? This is not always easy, but I could answer this question if I knew both:
a) how much coffee people drink (as a volume) in the U.S. on a given day,
b) the volume of a swimming pool.
If I divide those two answers, I have my solution. Let’s tackle (a) first:
I know there are roughly 350 million people in the U.S. Let’s assume kids don’t drink much coffee, so we ignore 20 percent of the population. Let’s also guess that half of U.S. adults don’t drink coffee at all. These are my assumptions, and I state them explicitly so that I can go back and change them later if I need to. And, even though we are talking about adults who drink coffee, each person drinks a different amount on a daily basis. Therefore, let’s assume that on average everyone has 3 coffee drinks a day. That leaves us with:

Now, I assume a coffee is a standard U.S. cup of coffee, and I know that a cup is 8 oz, but the solution will be easier to deal with if we are working with metric units. Let’s estimate that it takes 4 cups of liquid to fill a liter bottle. So, for my back-of-the-envelope calculation, 4 cups coffee is ~1 L of water. Notice that this is what I could do without any references handy so you might have a cleaner way of doing it.
We are thus dealing with: 1.05 x108 L of coffee. And for pure water at room temperature, I know that 1 L of water is 103 cm3 or 10-3 m3. We thus have about 105 m3 of coffee.
Now, let’s tackle (b), how much water is in a swimming pool. I honestly have very little concept about how large a swimming pool is but I do know the standard pool is an Olympic swimming pool. I’d guess it to be 10 m wide, 25 m long, and 4 m deep. That would be a volume of:
10 m ∙ 25 m ∙ 4 m = 1 x 103 m3 for an Olympic swimming pool
And, dividing these two quantities we arrive at:
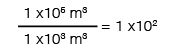
or approximately 100 Olympic-sized swimming pools of coffee.
While this doesn’t tell us exactly how many swimming pools we’d need, it really doesn’t matter if we are a couple off. We wanted to know about how many we’d need, just like we wanted to know about how many piano tuners we have in Chicago. Keep in mind that my answer is only as good as my assumptions, but we should expect the order of magnitude to be about right. And if I am good, I got us to within a factor of 2: somewhere between 50 and 200 swimming pools full of coffee.
These back-of-the-envelope calculations can help you simplify very complex systems to basic principles and help you come up with an estimate of what one might expect. Personally, I’ve been asked to do these kinds of questions in many job interviews, my thesis defenses, and even during talks I’ve given.
Your turn!
This example is left as an exercise to the reader:
How many cats are sleeping in the United States right now?
Submit your answer to sps-programs [at] aip.org with the subject line, “Sleeping Cats.” //
