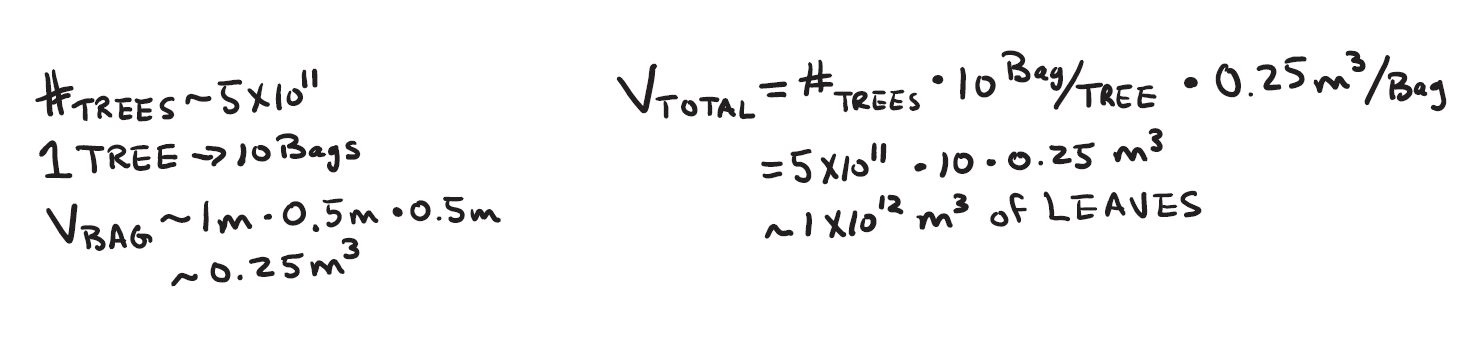Don’t Leaf Me Hanging!
Fall
2023
Physics Puzzler
Don’t Leaf Me Hanging!
Brad R. Conrad, Director of SPS and Sigma Pi Sigma
If you leaf near a forest or in a relatively wet climate, you know how big a task it can be to rake up all the leaves that fall in people’s yards each fall. Well, not all the leaves, as it’s good to leave some leaves around, but most people rake up most leaves each season.2 We’re so excited to see the leaves change color each year—and so much less excited to clean them up. As I spent the last 20 hours raking the leaves of only seven trees, it got me thinking about a new Fermi question…
Fermi Question:
If I raked up all the leaves on earth, would I have a literal mountain of leaves?
The physics of how materials like leaves make piles or stacks is extremely complicated—more mathematically complicated than Introductory Quantum Mechanics (as I’ve taught that class for many years, I can make a pretty solid claim). As “proof” I’ll reference XKCD comic #1867 in Fig. 1.
To solve most Fermi problems like this, we first need to reframe it in terms of questions we can try to answer. It’s even better if we can break it down into smaller problems. There are, as always, lots of ways to try to get a handle on this question, but here’s how I went about it.
Break it up!
I propose we break this problem down into three separate questions:
- How many trees are there?
- How many leaves are created by these trees that need to be raked?
- How big of a pile can we make with that many leaves?
How many trees?
The world is a really big place. I remember how big it is from a favorite professor of mine: Within a small margin of error, the radius of the earth is 2π⋅1000 km, or about 6,400 km. We know that the earth is about two-thirds water, so let's pick one-third. It’s a guess, but it’s probably not that far off—that’s a key method of solving Fermi problems. If you’re within a factor of 2 or 3, you are doing well. Let’s also estimate that each tree has a footprint of 100 m2. That leaves us with (I’m trying to make as many leaf puns as possible in this article) Fig. 2.
fig2.png

Figure 2. A calculation of the number of trees on earth using order-of-magnitude estimates. This calculation gives an area for earth of about 5 x 1014 m2. Assuming the earth is one-third land, the land is one-third trees by area, and each tree has a canopy area of 100 m2, we arrive at 5 x 1011 trees.
How many leaves?
I’ll be honest. I first tried to guess how many leaves were on an average tree, but it got pretty complicated. (I later found an article from The Physics Teacher that has a pretty neat way of estimating it.3) Complicated can be fun, but let’s not for this one. Instead, let’s think about this: If all the leaves from a tall tree fell, how many big bags would I need? Remembering my 20-hour comment for only seven trees, it’s definitely more than one bag and less than 100. I’d say it’s much closer to 10 bags. Each bag is about 1 m tall, 0.5 m wide, and 0.5 m deep, or 0.25 m3 in volume. So, putting all those numbers together brings us to Fig. 3.
How big a pile?
Since we are piling together so many bags of leaves, I’m going to guess they will stack as a 45° cone. I don’t have a good sense for whether this is right, but I think it would be at least 30° and less than 60°. From high school geometry, remember that the volume V of a right circular cone is V=(hπr2)/3. Solving for the height leads us to Fig. 4.
Solving for the h, we get a height of about ~11,000 m. For comparison, Mount Everest is 8,848 m tall. We should expect a whole lot of compression, as the weight of that many leaves will be immense, but even if it compresses by a factor of 4, it’s still a very tall mountain. So, the answer is yes. If I took all the leaves, I’d be able to make a literal mountain.
But... there is always one more problem to solve. I leaf you with this (I got one more pun in).
Challenge Fermi question:
If I jumped from a plane and landed on the pile, would the mountain (or hill) of leaves save me?
References
- For some reason, my original wording of the title, “How Many Leaves Fall in Fall?” didn’t quite leaf the right impression.
- Brooke Franklin, “This Fall, Leave the Leaves!,” US Department of Agriculture (blog), October 17, 2022, usda.gov/media/blog/2022/10/17/fall-leave-leaves.
- Larry Weinstein, “Solutions for Fermi Questions,” Phys. Teach. 56 (October 2018): A489–A489, doi:10.1119/1.5055310.