Puzzler_fig-1.jpg

Figure 1. A dizzy astrophysics student. All images by Brad R. Conrad.

I think many of us agree that space is cooler than cool. Ice cold even… It’s got almost everything we could want to study. But it’s really expensive to put instruments and materials into space—literally thousands of dollars per kilogram!¹ Part of the reason is that we burn a lot of expensive fuel along the way. Some people, including those at the company SpinLaunch,² are exploring much cheaper ways of doing this. So here's the question:

Could we use a large centrifuge to spin something and, like a slingshot, just throw things into orbit around the earth?

I mean, SPS is the society for physics AND astronomy students, right? 

How in the world (ha-ha) can we get a handle on a question like this? As students who have taken first-year physics courses might say, we need to know how much energy that would take. But they might also say that determining that is a little complicated. We spend lots of time in introductory physics (and parts of differential equations and advanced mechanics) discussing the importance of air drag. We know that it gets stronger as the speed of an object increases, from proportional to velocity at slow speeds to velocity squared at faster speeds (see Fig. 3).

12-Puzzler-2.jpg

Figure 2. A spherical space cow, SPS’s unofficial mascot.

We also know that if we drop an object like a sphere from a really high place, initially it will accelerate quickly because it is attracted to the earth. This phenomenon is described by Newton’s law of gravitation.

As an illustrative example, let’s say we drop something from the tallest building on the earth (see Figs. 4 and 5). Currently, that record is held by the Burj Khalifa skyscraper in Dubai, United Arab Emirates, which is 828.0 m (2,717 ft) tall. For context, it’s about 1.5 times as tall as One World Trade Center in New York City and almost nine times taller than the Statue of Liberty. It’s pretty darn tall.

Puzzler_fig-3.jpg

Figure 3. A person experiencing air drag. The force due to drag for slow speeds is D_slow ∝ v and for fast speeds D_fast ∝ v². The drag equation is also given.

Using some of the information in Fig. 4, how fast does the object accelerate when it starts to fall from the top of the building? 

Once you determine the answer, consider this question: Does the height of the building strongly affect the downward acceleration?

When it starts to fall, the acceleration of the object is very close to what we calculate at ground level. You should get a difference of significantly less than 0.1%. But, more to the point of our initial puzzle, what would the
acceleration be for an object at NASA low Earth orbit (LEO), or about 200 km above the surface of the earth?⁴ 

This is a really important question, because when something is in orbit, it is continually falling around the earth. 

Puzzler_fig-4.jpg

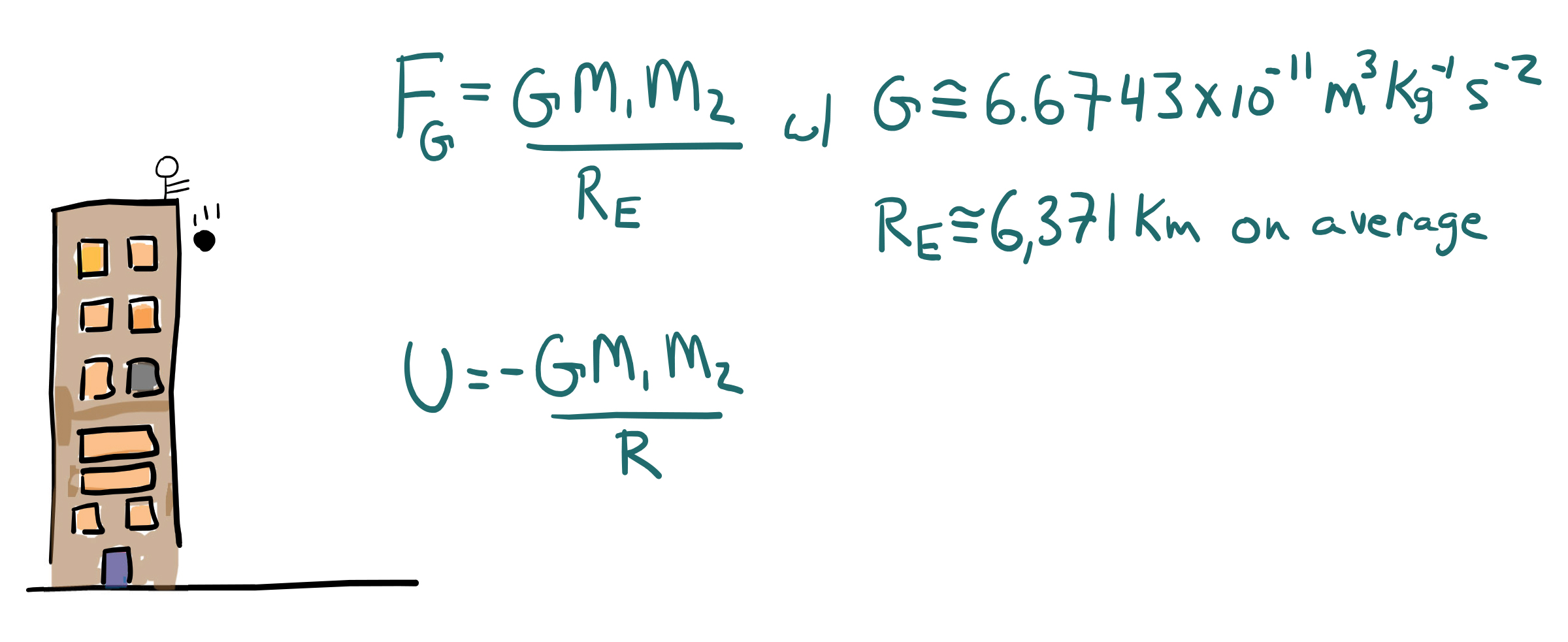
Figure 4. Newton’s law of gravitation describes a dropped object falling. Here, G is the gravitational constant,³ M₁ is the mass of the first object (the earth), M₂ is the mass of the second object, and R_E is the radius of the earth. The figure also shows the equation for gravitational potential energy U, where R is the distance between the two objects.

When we (theoretically) fire a cannon ball along some long path, the ball has to fall a little further down at the end of the path because of the curvature of the earth—the earth’s surface is literally farther away from the trajectory of the cannonball. This becomes substantial for long distances, making the path of the cannonball a lot longer because it falls more. 

Similarly, if something is in a spherical orbit, the earth’s surface keeps moving away at the same rate the object is falling toward the earth because of its curvature. It’s helpful for me to think of an orbit as continually falling. This idea helps us get one of the two key pieces of information we need to solve the energy problem: How fast would the object need to travel to keep falling around the earth at LEO altitude? 

I suggest starting with Newton’s second law and the definition of centripetal acceleration. You should get something a little smaller than 8.0 km/s, which is about 23 times the speed of sound in air. NASA and other space organizations use such a high altitude because the atmosphere is significantly less dense and the air drag decreases a lot.

Puzzler_fig-6.jpg

Figure 6. A zoomed-in sketch of an orbit showing that the earth is falling away from the object.

Now let’s get the second key piece of information: How much energy would it take to get the object from the earth’s surface to LEO orbit?

We need to get our object up to a LEO altitude! The other half of the problem does set a high bar (ha-ha). While we could do a bit of calculus, we can actually use the information we already have and think in terms of potential energy (see Fig. 6). Interestingly, it requires significantly less energy to get the object up than it takes to speed it up to about 8.0 km/s.

Now it’s time to put everything together. Using only what we’ve gone over here and a few modest assumptions, can you solve the puzzle?

If we used a large centrifuge, how fast would we need to spin the object to give it that much energy? Is that a reasonable approach?

12-Puzzler-5.jpg

Figure 5. Burj Khalifa reaches into the sky. Photo by Riyas Mohammed on Unsplash.

References

1. “Space Launch Market Competition,” Wikipedia, en.wikipedia.org/wiki/Space_launch_market_competition, accessed 2/12/2024. 
2. Check out SpinLaunch's idea on YouTube at youtube.com/watch?v=RiALARM1xv0. 
3. NIST, the National Institute of Standards and Technology, supports and provides standards and references for the United States, including work on fundamental constants such as the gravitational constant G.
4. Visit the Wikipedia article on low Earth orbits at en.wikipedia.org/wiki/Low_Earth_orbit.