Now Let Us Consider . . . a Herd of Spherical Cows?
Fall
2021
Physics Puzzler
Now Let Us Consider . . . a Herd of Spherical Cows?
Brad R. Conrad, Director of SPS and Sigma Pi Sigma
During a planning session for our upcoming Centennial Physics Congress in Washington, DC (October 6–8, 2022), an immensely important puzzle came up:
Theoretically, how many spherical cows could fit into Washington, DC?
A ridiculous question? Definitely. Although you never know when you might need ridiculous information at your fingertips, and this definitely isn’t something you can look up.
An answerable question? Totally.
First things first—What would we need to know to make a good estimate?
How big is a spherical cow?
How do we pack them in DC?
Puzzle 1: How big is a spherical cow?
You probably won’t find this in many physics textbooks (but possibly in a theoretical animal science or quantum farming course...). I’ll assume we’re talking about dairy cows. I have seen them in person, and these cows are way bigger than me but also smaller than a standard US car. I’ll estimate they weigh 450 kg (which is about 1000 lb in the imperial system). THAT. IS. HUGE. We’re talking several football/soccer players big.
I’ll assume cows are mostly water (since humans are), and one of the few facts I’ve memorized is the density of water at STP: 1000 kg/m³. This is helpful because volume is mass divided by density, as you might remember from middle school. We also know that the volume of a sphere is 4πr3/3, , where r is the radius of a sphere. Combining those equations for volume yields the following:
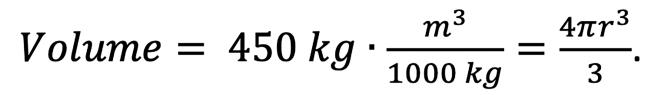
Solving for the radius r, we arrive at about 0.475 m as the radius of our spherical cow.
Now we just need to know how many spheres of radius 0.475 m fit into Washington, DC. From Fig. 1 we can see that Washington, DC, is roughly a diamond shape. I’m guessing it’s about 10 miles per side, or 100 square miles, minus the land given back to Virginia (on the west side of the Potomac River).¹ If we take out the water and now-Virginia part of the diamond, we can estimate the land to be about 67 square miles, or 173 km².
 Puzzle 2: How do we pack them in DC?
Puzzle 2: How do we pack them in DC?
If we really packed our spherical cows in there, they’d be touching each other. Just how tight could we pack them? Gauss and Lagrange determined the maximum packing of spheres in a 3D volume and on a flat 2D surface²—in fact, it’s a common calculation in condensed matter physics because it directly relates to crystal structures! If we put in as many cows as possible without stacking them, they’ll naturally form a hexagonal pattern, as shown in Fig. 2.
From this image we can see that for circles of radius r and a hexagon of side length 2r, the spheres fill this fraction of the space:
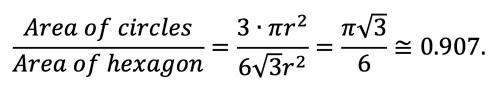
This is independent of sphere radius (which is super cool) and means that when we pack the cows in, we are left with about 9% empty space. If we ignored buildings, elevation changes, small rivers, and everything else already in Washington, DC, we’d be able to fit about 349 million spherical cows! That’s a lot of µ-ing (bad joke).
Next, I challenge you to think outside the two-dimensional world: What if we could stack the cows? How many spherical cows could we stack inside Washington, DC?
Hints: The final shape would probably be something like a pyramid. Check out the awesome Fall 2017 Puzzler written by Gary White for some useful insights.³
References:
1. It turns out this was a very good guess, as it originally was 10 miles per side. The actual area is about 68.3 mi2.
2. Zamponi, F., “Packings Close and Loose,” Nature 453 (2008): 606–607, https://doi.org/10.1038/453606a.
3. G. White, “Consider a Circular Cow,” The SPS Observer, Fall 2017, http://www.spsnational.org/the-sps-observer/fall/2017.
Willing to share your answer? Please email SPS-Programs [at] aip.org with a one-page PDF showing how you solved the above question. Submissions have a chance to be highlighted on SPS National social media pages, and participants may receive some SPS swag!
