Do You Want to Build a (Colossal) Snowman?
Spring
2021
Physics Puzzler
Do You Want to Build a (Colossal) Snowman?
Brad Conrad, Director, SPS and Sigma Pi Sigma
I’m sure people will use a flurry of different methods to solve this puzzler! This question is an extension of an actual fifth grader’s question at an “Ask anything” session during an outreach event in Florida. The student asked, “How big could you build a snowman?” to which I replied, “Well, it depends on how much it snowed!”
Breaking it down
While the material science of snow is extremely interesting,1 I propose we break this problem down into two separate questions:
1. How much snow do we have to work with?
2. If I could collect all that snow, how large of a snowperson could I make?
As with any good back-of-the-envelope calculation, we should also state the assumptions. As we go along, I’ll note those in italics.
How much snow do we have to work with?
This is probably the hardest part of the problem because it involves so many assumptions! If we’re going big, I’d collect all the snow from an entire snowstorm. That means I’d first need to estimate the volume of snow produced by the storm. Doing so requires two things: the surface area covered by the storm and the average depth of snow. From growing up at a higher latitude, I would guess an average snowstorm drops four inches of snow and covers a really big area—something like several US states.
But, as anyone who’s ever made a snowball knows, snow compacts a lot when compressed.2 Let’s assume it compresses to a quarter of its volume (2.1 × 1010 m3).
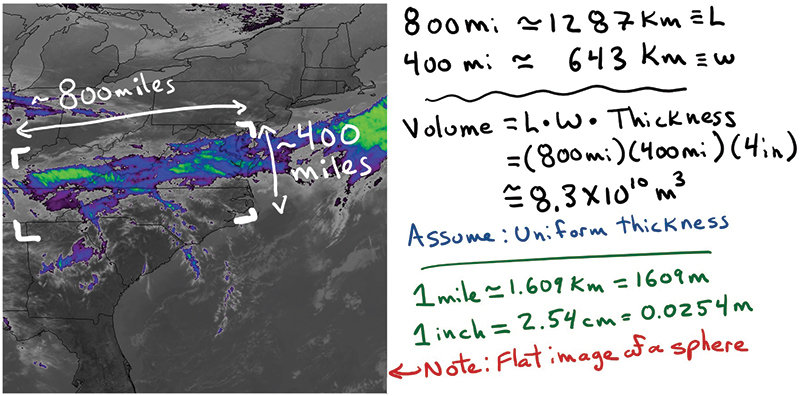
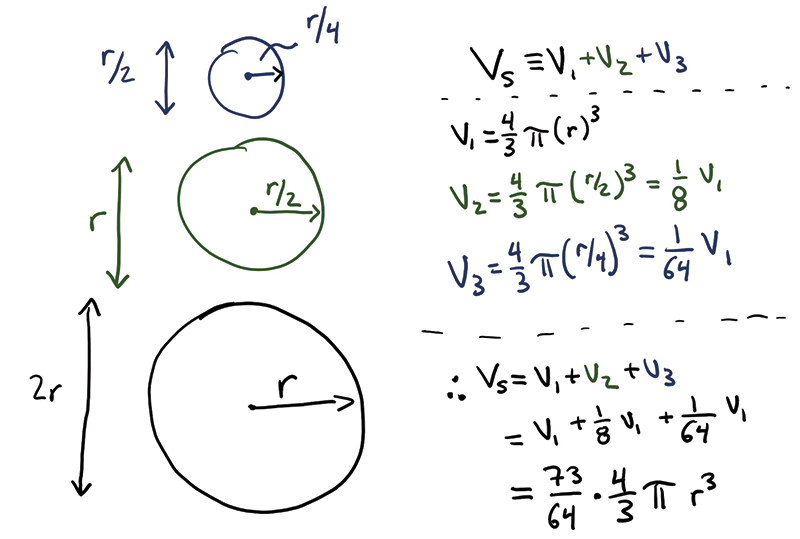
Well, how big of a snowperson can we make with that much snow?
The tallest snowperson on record had more of a cone shape, but let’s assume we can engineer a snowperson from three spheres. Let’s also assume that each sphere is half the diameter of the lower sphere.
We can now pull it all together, since we know the volume of compacted snow V and the volume of the three-sphere snow VS. By setting them equal to each other and solving for the radius, we get a height of 3.5•1640 m, or about 5.73 km. For comparison, Mount Everest is the tallest mountain in the world at about 8.85 km.
Your turn!
In this calculation, I made a pretty rough estimate of how snow compacts. In reality, the snow would compact A LOT, and most of it would become ice through melting,2 which has a different packing ratio. Also, I assumed a three-sphere snowperson. For comparison, the tallest snowperson ever constructed was about 34 m tall and had a cone shape—which, in terms of mechanics, is a much better design. If we took these factors into account, what height could we expect?
References:
1. Henri Bader, The Physics and Mechanics of Snow as a Material, Cold Regions Research and Engineering Laboratory, 1962.
2. Angela Herring, “The Physics of a Snowball,” News@Northeastern, January 2, 2014, https://news.northeastern.edu/2014/01/02/the-physics-of-a-snowball/.
3. “Austria Breaks Record for World's Tallest Snowman,” DW, February 2, 2020, https://www.dw.com/en/austria-breaks-record-for-worlds-tallest-snowman/a....
Check out our answer at spsnational.org/the-sps-observer.
