Chasing Rainbows, Part 2
Spring
2017
Physics Puzzler
Chasing Rainbows, Part 2
Donald Simanek, Emeritus Professor of Physics, Lock Haven University of Pennsylvania
Lock Haven University

In the last issue of The SPS Observer we tried to answer the question: How far away is a rainbow? See "Chasing Rainbows, Part 1".
We concluded that a rainbow is a real image, despite being made up of just reflected light. And we argued that an image of a rainbow—much like your reflected image in a mirror—must be farther away from us than the reflective surface that created it.
But, you may say, "I can form a rainbow with a water sprinkler. The water drops are only a few feet away, and I can see the rainbow between myself and a bush. Surely the rainbow must be nearer than the bush."
Think again of the image formed by a mirror. It appears farther away than the mirror. If we triangulate the water sprinkler rainbow, we find it is much farther away than that bush. This, like many optical illusions, produces cognitive dissonance, for several clues we use for determining distances seem to be giving contradictory information.
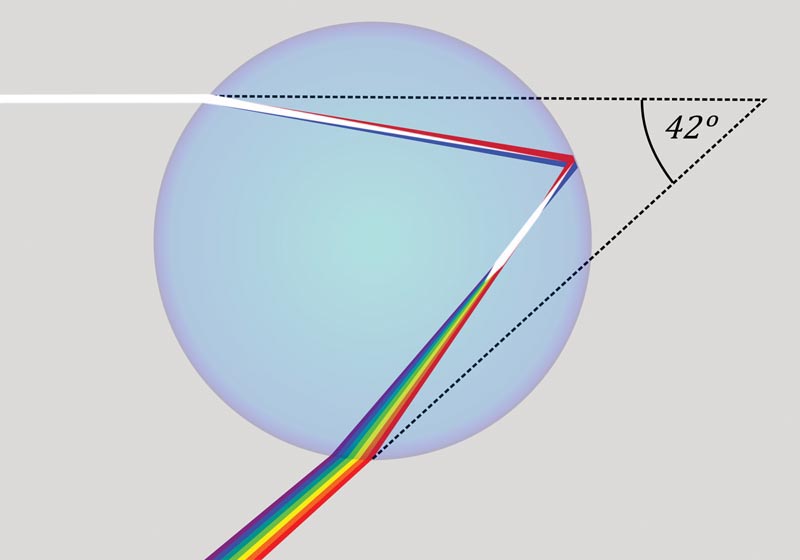
Is the cloud of water drops acting like a mirror? Not exactly. The drops capture light from the sun and reflect it internally, and the light emerges going in the opposite direction but deviated 42° (for red light). This is the reason the rainbow arc has a radius of 42°, centered on the antisolar point, a point determined by a straight line from the sun through your eye.

In fact, the light from any small portion of the rainbow is coming from drops over a wide range of distances, all the way through the cloud, perhaps several miles, not from a simple plane mirror surface.
Now you might suppose that the size and shape of the individual water drops, each acting as a tiny lens, might determine the apparent distance to the rainbow image. Surprisingly, they do not. The sun is so far away that its light reaching the earth diverges very little. Rays from any point on the sun are nearly parallel when they reach the earth. So all drops receive rays from nearly the same direction, and redirect them back to our eyes, still all nearly parallel. A small caveat: the sun is not a point source of light. It subtends an angle of about 0.5° as seen from earth, but this doesn't compromise our argument. It only adds a slight blurring to the rainbow image.
The bottom line is that the rainbow is as far away as an image of the sun would be if reflected by a huge plane mirror at the distance of the cloud of water drops. So "as far away as the sun" is the best answer. But other answers are close enough.
If you accept the rangefinder definition of distance, this result would be confirmed by direct experiment, by sighting the rainbow simultaneously from two widely separated vantage points.
Now that you understand how the rainbow is formed, you know the answer to the question "Why is the center of any rainbow formed by sunlight always below the horizon?" It is simply because the sun is visible only when it is above the horizon. The rainbow's arc is always centered on the antisolar point—on the shadow of your head. You now also know why no one has ever found that pot of gold. There wouldn't be enough gold in it to pay for the trip. And the rainbow would disappear as you passed through the cloud of water drops forming it.
Some nit-picky readers may note that the two lines from the sun through your two eyes diverge slightly, since the sun is not infinitely far away. This would put the rainbow's image just a smidgen beyond infinity. Now we get down to the psychology of vision. Binocular vision can tolerate a slight divergence of the two eyes (at least for most people). The divergence here isn't large. How large?
The sun is 5.89 × 1012 inches away. Human eyes are spaced about 2.5 inches apart. The divergence angle is therefore 2.43 × 10-11 degrees, approximately. You'd never notice such a small divergence. So infinity is close enough for practical purposes. Even with a large baseline rangefinder, of perhaps a mile, the rainbow image is still stuck pretty near infinity—infinity being defined here as greater than any measurable distance. One could also make a case for the fact that the horizon is usually so far away as to be indistinguishable from infinity seen with the naked eyes. But whenever you use the word "infinity" as if it were a number, you are on a slippery mathematical slope.
More Information
- Rainbow formation. The Physics Classroom.
- Rainbow stereoscopy. Science Animations.
- The mathematical physics of rainbows and glories. John A. Adam, Physics Reports 356 (2002) p. 229-365.
- All about rainbows, double rainbows, circular rainbows! Skulls in the Stars.
- Rainbow. Hyperphysics.
- Greenler, Robert. Rainbows, Halos and Glories. Cambridge Univ. Press, 1980.
Feedback
Feedback is appreciated from readers.
E-mail dsimanek [at] lhup.edu (Donald Simanek).
