Black Holes in The Key of B-Flat
Summer
2017
Feature
Black Holes in The Key of B-Flat
This activity lets students learn more about the universe and how astronomers study it. A bit of math is required, so this is better for more advanced students.
Note: This demonstration has been adapted from NASA’s Chandra Observatory. You can find more information at http://chandra.harvard.edu/learn_cxc.html.
MATERIALS:
Millimeter-scaled rulers, paper, and pencils.
INSTRUCTIONS:
Give students a copy of the images and a ruler. Tell them this story:
The Chandra X-Ray Observatory took these images in 2003 of a massive black hole in the Perseus galaxy cluster, 250 million light-years away.
Scientists did not expect to see the black hole, but they did expect to see the hot gas in the core of the cluster, heated to a million degrees and visible in the X-ray spectrum. However, instead of a blob of gas, they saw a series of concentric rings (more visible in the lower image, which has been enhanced), which astronomers determined to be sound waves. That's right: This black hole is “singing” in space.
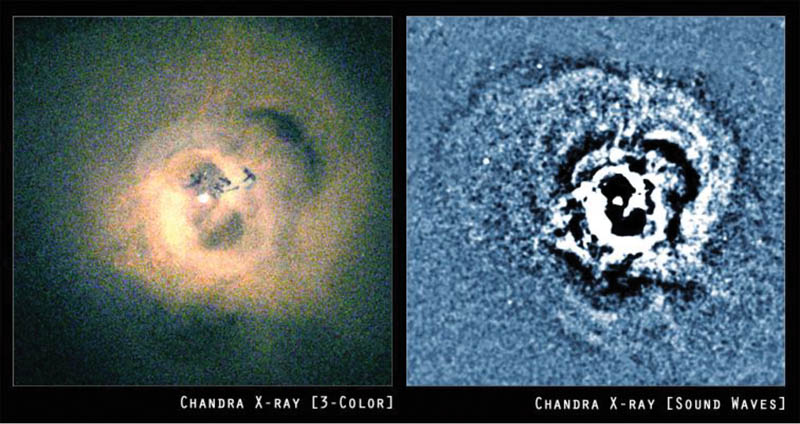
A 53-hour Chandra observation of the central region of the Perseus Galaxy Cluster (top) has revealed wavelike features (bottom) that appear to be sound waves. Make photocopies so all students have one, or you can print off copies of the image at http://chandra.si.edu/photo/2003/perseus/.
ASK THEM THE FOLLOWING QUESTIONS:
- The galaxy in the image has a physical width of 350,000 light years. What is the scale of the image in light years per millimeter?
- Based on the lower image, how far apart are the crests of the sound wave in millimeters?
- What is the wavelength of the sound in light-years?
- The wavelength of middle C on a piano is 1.3 meters. If 1 light-year is the distance light travels in one year, what is the distance between waves in meters?
- Each successively lower octave is twice the wavelength of the previous one. How many octaves below middle C is the sound given off by the black hole?
- Now, use what you’ve learned. If we use the entire earth as a detector, what is the lowest note we could observe? That is, how many octaves below middle C?
COMMON QUESTIONS TO EXPECT:
Can we hear the black hole?
No! Sound is a longitudinal wave and needs a medium. In this case it’s hot gas. Since the gas doesn't reach us, because the cluster is 250 million light-years away, we cannot detect it.
In addition, the sound produced is at such a low frequency that it's far beyond the limits of human hearing.
Why is it doing this?
Astronomers believe that bubbles in the cluster gas are blown out by jets from a supermassive black hole in the center. Those bubbles push against the gas, creating a pair of sound waves.
The waves also provide a source of energy for keeping the gas from cooling too much, which prevents star formation in the central galaxy. Scientists believe that to offset cooling in the cluster, it had to have been “singing” the same note for 2.5 billion years.
PHYSICS:
Multiply the scale you found in question 1 and the ruler distance between waves you measured in question 2. This will give you a wavelength in light-years, or the answer to question 3. A light-year is the distance light travels in one year. Thus in one year, light would travel 3 × 108 m/s · π × 107 s ≈ 9 × 1015 m. Note: We are approximating there are π times 107 seconds in a year. A distance between waves of ~3 × 104 light-years, or ~3 × 1020 m, is reasonable.
Once you have the distance between waves in meters, we want to know how many times you need to double 1.3 m (the wavelength of middle C on a piano) to get the length measured in question 2. Students can do this with calculators, on paper, or spreadsheets, but a result around 68 octaves below middle C is correct. Astronomers even calculated that the “note” the cluster is “singing” is a B-flat.
Bonus question left to the reader: If a piano has just over 7 octaves and is 165 cm wide, how big of a piano would you need to hit the note Chandra detected?
