Pedal Power Puzzlers
Fall
2019
Physics Puzzler
Pedal Power Puzzlers
Katherine Zaunbrecher, SPS National Council Member-at-Large, and Brad R. Conrad, Director of SPS & ΣΠΣ
“Life is like riding a bicycle. To keep your balance, you must keep moving.” — Albert Einstein
Bicycles have been around for 200 years and, in that short time, have completely changed the way we think about travel and how humans interact with machines.1 We can learn a lot about physics by thinking about bikes and cycling-powered human locomotion. Bicycles are also an amazing source of Fermi problems—sweeping questions that can be answered with a little physics, a little critical thinking, and some back-of-the-envelope estimates. For more on Fermi problems, check out the Winter 2017 puzzler.2

To get warmed up, let’s work a problem together. Note that our estimate demonstrates possible paths to the solution—not the only paths. One of the great things about physics is that it often allows us to reach a solution via several different paths.
What is the average output power of a person riding a bicycle?
The simplest path to power is to estimate the force needed to maintain a constant speed. First, let’s estimate the speed of a person riding a bike. Google Maps assumes an average speed of about 10 mph when giving the time estimate for how long it takes to get to a destination when using a bike.3 It turns out that this is totally reasonable, as it’s faster than walking, which is a few miles per hour, and slower than a car, which is about 60 mph. This also leads to a fun game—by how much can you beat the Google estimated arrival time?
Now, let’s relate this sustained velocity to power. From our first-year physics course, we remember that the power output P of a person on a bike is directly proportional to the force applied F, the bike velocity v, and the distance x over which the force is applied. These are quantities that we can estimate:
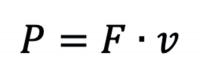
For completeness, let’s take a look at the units of this relationship.
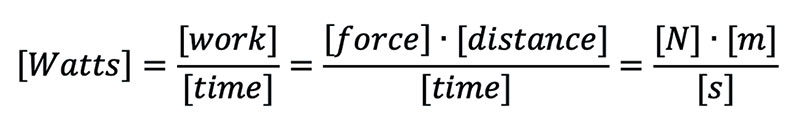
We can also think about this problem in terms of angular measurements, using the applied torque and angular velocity ω (since we’re talking about bicycles with circular wheels, for Newton’s sake!) to calculate power:
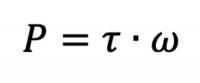
Again, let’s check the units for completeness and to ensure we’re going down the right path:
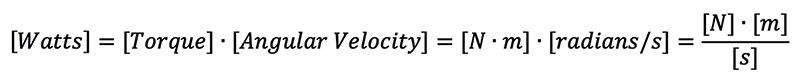
Note that radians is a dimensionless quantity, so it disappears in the line above. We can assume that an average comfortable strolling speed on two wheels is on the order of 1.5 rotations per second, which comes out to 3π radians per second. Remember, we just need reasonable estimates for these quantities. If we are off a little here and there, we’ll still be on the right track.
For the quantity radius r, we consider the length of the crank arm (the part attached to your pedal that transfers the motion to the chain), which is about 175 mm (7 inches).
Now we dive into the hard part of this approach: How do we estimate the torque? Or the force F applied to the crank arm?
We can assume that the laziest person in the world gets most of their help from gravity. When they place their legs on both of the pedals, the force exerted is their mass times the gravitational constant. Let us assume a mass of 15 kg per leg and 10 m/s2 for the acceleration due to gravity. We also know that the applied force will be sinusoidal since the torque applied is a cross product with a magnitude that depends on the angle θ between the crank arm and the force applied by the leg:
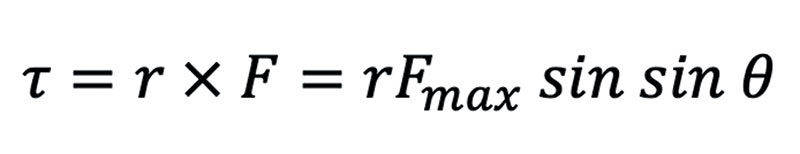
Thus, when one of the pedals is at the top of its motion, the force and momentum of the crank arm are parallel and there is no torque. We’ll call this angle zero. But as the crank arm continues to move around, the angle increases and the torque increases. When the crank arm and leg are π/2 radians apart, the instantaneous force is at its maximum. The torque then decreases until the pedal reaches the very bottom of the rotational path (at π radians). If you assume a sinusoidal model for force, you can estimate the average force Fave as the integral of the sine wave from zero to pi:
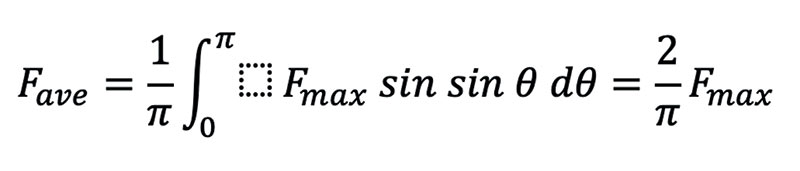
Thus the average force Fave from one leg of a person is
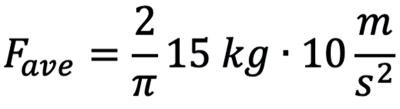
which is about 100 N. Therefore we can put it all together and write out the average power as

Now that you’re warmed up, it’s time for the physics puzzler:
A person wants to ramp over the Mississippi River on a bike. How fast would an adult human have to go on a bicycle and at what ramp launch angle to make it across the Mississippi River and land in New Orleans?
Hint: From New Orleans you can see people on the opposite riverbank, but they look small. Try to answer this without looking up anything on the web.
Extra puzzler challenge:
Bikes are more stable when moving forward without a human on them. Why?
Hint: Seriously, they are.
After you write down your logic, check out the minutephysics video “How Do Bikes Stay Up?”4 There are studies that explain that the popular gyroscopic answer is mostly a myth.5
Other puzzles you can try:
- Which brake provides better (higher) braking power, front or back?
- Rotational motion requires friction, so what is the maximum acceleration of someone on a bike without flipping?
- How many street tacos would you need to eat in order to power a ride from NYC to LA?

References:
1. Herlihy, David V. Bicycle: The History. New Haven, CT: Yale University Press, 2004. p. 26. ISBN 978-0-300-12047-9.
2. Conrad, Brad. “A Physicist’s Best Friend: Fermi Questions.” SPS Observer (Winter 2017).
3. www.ilovebicycling.com/how-accurate-are-google-maps-cycling-directions, Retrieved August 12, 2019.
4. https://www.youtube.com/watch?v=oZAc5t2lkvo.
5. Sheppard, Alyson. “The Physics of the Riderless Bicycle.” Popular Mechanics (April 2011). https://www.popularmechanics.com/adventure/sports/a6602/physics-of-a-rid....
