Consider a Circular Cow
Fall
2017
Physics Puzzler
Consider a Circular Cow
Gary White, SPS Advisor, The George Washington University, gwhite [at] gwu.edu
When herding cattle,1 physics folklore suggests that it is occasionally useful to consider the concept of packing fraction p, defined here as the ratio of cow volume to total corral volume. Analytical results regarding the optimal packing arrangements for cattle in a corral are usually reported only under the vastly freeing assumption of bovine sphericity, and usually with some cheekiness or even outright smirking. Here, we seek to relax slightly the perfectly spherical supposition to include the addition of certain round appendages, while gleefully restricting our gaze to only the 2D case—or, in other words, viewing the corral from directly overhead. Thus, we “consider a circular cow” with certain circular appendages and the associated packing fraction, roughly as shown in Fig. 1, but not before surveying a tiny bit of the rich background of this celebrated problem.

Beyond modern physics and solid state physics courses, the question of determining the maximum packing fraction of perfectly spherical cows in three dimensions has a long and storied history, dating at least back to Kepler.2 He speculated, but had no proof, that the best packing fraction in 3D was the one in which the first layer is placed in a hexagonal configuration as in Fig. 4 (not the square configuration of Fig. 3), and subsequent layers were similarly arranged in hexagonal rafts but shifted so that spheres settle into the “low spots” between the spheres below them, much like oranges are stacked into pyramids in a grocery store. This arrangement can be shown to have a packing fraction to have a packing fraction p of 1/6 a cow volume (radius R) per tetrahedral pen volume (of side 2R), or
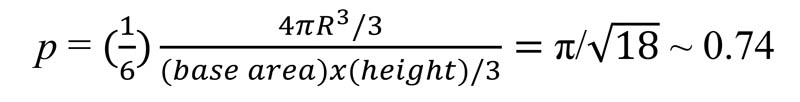
This means that for a given (large) pen, perfectly spherical cows take up about 74% of the space. The rest is empty space. Gauss took a stab at proving this result and showed that among lattice cattle arrangements Kepler’s is the best, but that still left the seemingly unlikely possibility that irregular or random arrangements might be better. The question remained unresolved for many decades, and in 1900 Hilbert included the sphere packing problem among his famous 23 unsolved problems. Finally, in 2014, more than 400 years after Kepler’s investigations, Hale and collaborators published a formal proof, verified by automated proof-checking software. Due to the complex nature of the proof and its unorthodox validation, however, some might say that there is still a flyspeck of doubt. In another fairly recent twist, Paul Chaikin and his collaborators, including undergraduate researchers, have reported4 that when ellipsoidal cows (think almond M&Ms) are randomly packed into a corral, the resulting packing fraction can perhaps be even higher than the Kepler arrangement (still about 0.74 or so), shocking the agricultural world, not to mention attentive confectioners. But perhaps even more exciting is the very recent triumph of Maryna Viazovska in 8 dimensions. She has proven, in a real tour de force paper, that the best packing fraction possible for 8D spherical cows is p = π4/384 ~ 0.25! Apparently, when packed into corrals of higher dimension than our meager three, there’s a lot more empty space for the herd, even when packed as tightly as possible.
Visualizing 8D spherical cows and the subtleties of their packing is beyond the abilities of this author, however, so I’ll return to what motivated this little reflection. Recently I attended an SPS intern event where a collection of the SPS cows (see Fig.1) were splayed out on a table, and the question arose organically: How tightly could these cows be packed without overlap? Clearly, more than a perfect circle was needed to do justice to this magnificent animal! Perhaps appending a rect-angular head and a semicircular udder would be enough detail to start, completely ignoring the legs and tail, but even that seemed impossibly complicated, especially given that it took 400 years to get spheres alone!
So, in this treatment we deviate only modestly from the classic problem of perfect circle packing to consider what happens if you add an appendage or two, such as a head, with the constraint that it also has circular form, tangent to the larger circular body. It turns out that this type of two-circle problem has been pondered at some length already, but not precisely in the cattle context in which we are interested, so let’s see how these results apply to our situation. Tom Kennedy6 showed in 2006 that there are only nine possible values for the radius ratios in the compact two-circle problem—two of these nine can be represented by the configurations we visited before in Figs. 2 and 3.
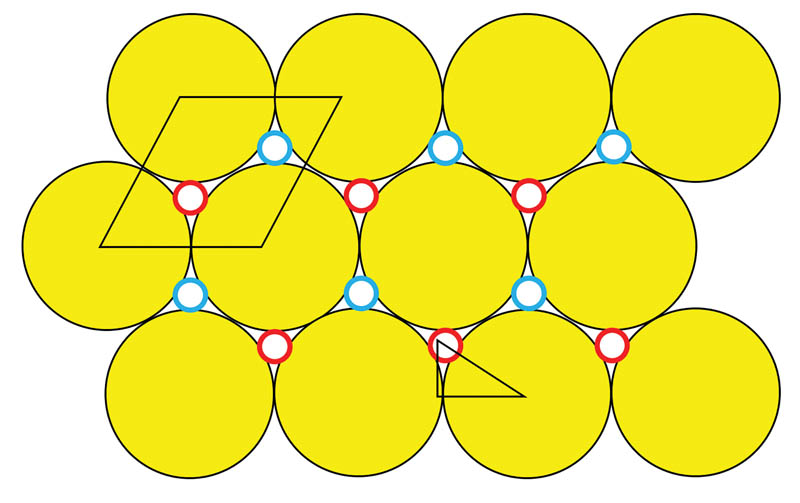
First, let’s take a look at the seemingly most obvious lattice arrangement in 2D, the square lattice shown in Fig. 2, ignoring the red circles and creepy cow eyes for now.
The large yellow circles represent our circular cow bodies, and we imagine that each cow body has a circular cow head up and right from the body (six heads are shown in red in Fig. 2), which we will be adding into the mix presently. We see by considering the square (which has side 2R, where R is the radius of the yellow circles) in Fig. 2 that the packing fraction for this arrangement of yellow circles is simply the area of the yellow parts within the square divided by the area of the square:
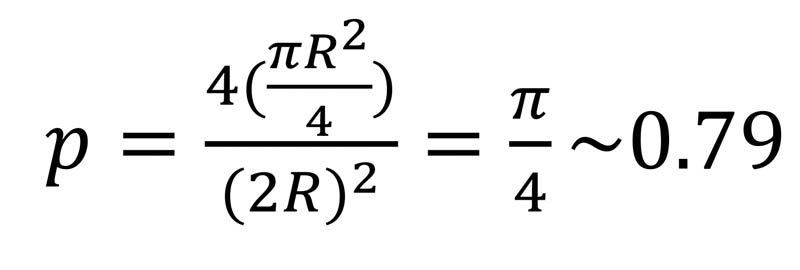
But if we add in a circular cow head as shown we get a higher packing fraction: since the little circle outlined in red with radius r must satisfy (r+R)2=R2+R2 according to the triangle shown in Fig. 2, we have r=(√2-1)R, so we get a new packing fraction, for a circular cow with a circular cow head, of
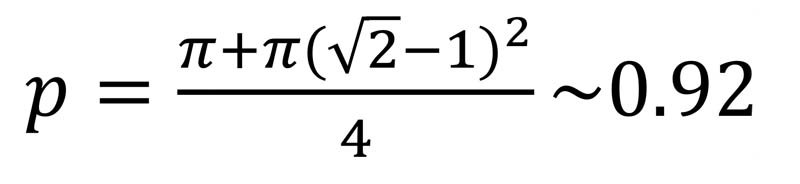
The packing fraction for the hexagonal lattice shown in Fig. 3 is obtained by considering the parallelogram-shaped unit cell: the yellow area within it is again πR2, but the area of the pen itself is now only 2√3R2. Thus, the packing fraction for the big yellow circles in this hexagonal array is then
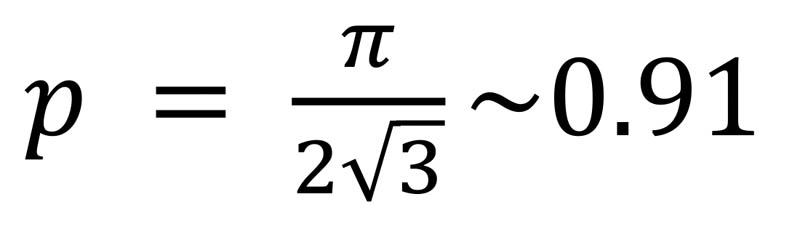
considerably larger than the square lattice with no heads. Adding in the small red-outlined circle as a (tiny!) circular cow head gives an extra area of πr2, where r can be shown by similar geometric considerations as above to be given by
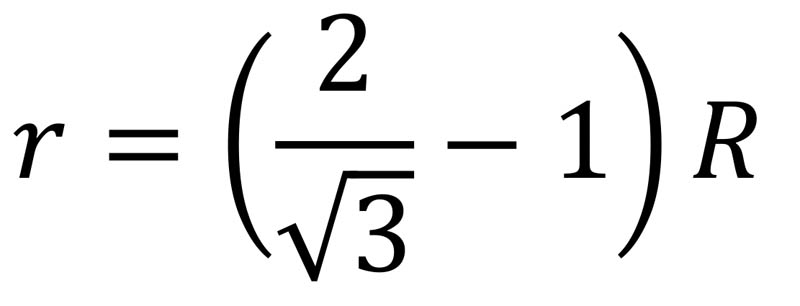
So the packing fraction for the hexagonal array with one cow head becomes
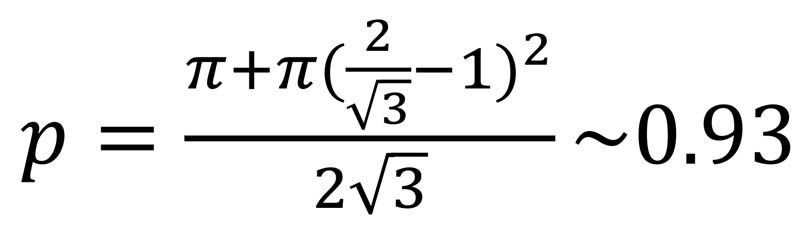
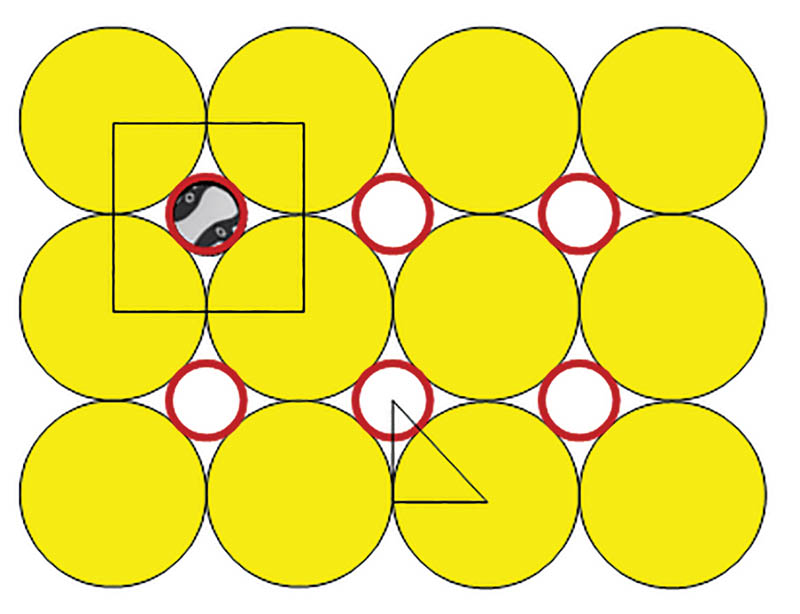
If a second head is evident on each cow (like the two-headed calf that always seemed to be a staple at the state fair), then the packing fraction gets another contribution from the area of the little blue circles as well and goes up to
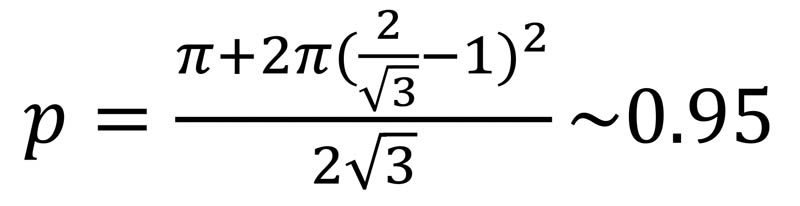
Finally, among the other nine possible values of radius ratio, examination of the corresponding circle patterns in Ref. 5 shows there is only one other that corresponds to a one-headed cow, and it can be represented by the configuration shown in Fig. 4.This makes an excellent physics puzzler to leave you with: what do you get for the packing fraction of the arrangement in Figure 4? I find it to be slightly less than that of the one-headed version of Figs. 2 or 3. Feel free to email me with your solution. So it seems that among circular cows with one tangent circular head the best lattice packing fraction is 0.93, that of the hexagonal lattice with the red heads in Fig. 3. If you want to allow two-headed cows (or if the second circle represents some other body part), then p ~ 0.95 (Fig. 3, with the red and blue circles) wins out…at least that’s what I get. There are several other two-headed cow possibilities among the nine allowed ratios, and some three- and six-headed possibilities as well. Check it out—it’s fun stuff! As to the fine details of the packing fraction of the actual official SPS cow in Fig. 1, that awaits a more careful treatment that includes blocky heads and other, more adventurously shaped appendages, by some enterprising young scholar.

1. I was not able to identify the first reference to the spherical cow meme, but other animals are similarly mistreated, including a “famous story” about a spherical chicken appearing as a letter in Science 28 Dec 1973 [182(4119):1296 (1973)] by Steven Stellman. Back in 1952, Alan Turing referred to the lack of spherical symmetry in horses in his article The Chemical Basis of Morphogenesis [Philos. Trans. R. Soc. London, Ser. B 237(641):37–72 (1952)], though it is difficult to gauge the level of humor intended. Frequent air travelers today might speculate whether the airlines have leveraged some human-spherical-packing-fraction-in-cylinders models in their determination of modern flight legroom dimensions.
2. Kepler, Johannes, Strena seu de nive sexangula (The six-cornered snowflake) (1611). Kepler, along with contemporaries Thomas Harriot and Sir Walter Raleigh, apparently was interested in how best to stack cannonballs.
4. Donev et al., Science 303(5660):990–993 (2004).
5. Viazovska, M., The sphere packing problem in dimension 8, Ann. Math. 185:991–1015 (2017), arXiv:1603.04246 , doi:10.4007/annals.2017.185.3.7.
6. Kennedy, T., Compact packings of the plane with two sizes of discs, Discrete Comput. Geom. 35:255–267 (2006), https://doi.org/10.1007/s00454-005-1172-4.
------------------
To purchase spherical cow stickers (as depicted in Fig. 1), SPS coffee mugs, and other SPS merchandise, visit the online SPS store today – https://aipsps.site-ym.com/store/default.aspx
